Vector Addition using OpenAI Triton - Part 2

This is the second blog in the series of blogs for implementing OpenAI Triton Kernels.

In the last blog we covered the following:

• Basics of Triton language.
• Offset calculation intuition.
• 2D Vector Addition kernel implementation

In this blog we are going to implement the same 2D Vector Addition using different BLOCK_SIZE to gain more command over pointer arithmetic. We are also going to compare the performance of different implementations against the pytorch version.

In the previous implementation we were setting the BATCH_SIZE = triton.next_power_of_2(ROW_SIZE). This made the implementation pretty straight forward however this is not an efficient implementation. We will see why later in the blog. For now let’s implement a kernel using a BLOCK_SIZE < ROW_SIZE. We are going to set BATCH_SIZE = 1024. We will see 2 approaches.

1. Parallelize across Rows (like the 1st implementation)
2. Parallelize across BLOCKs.

Implementation 1 - Parallelize across Rows.

Driver Function

Since we are going to parallelize across rows, then the number of grids will be number of rows M. This means there are going to be M instances of the kernel computing the vector addition.

Here’s the Driver function:

def add(x: torch.Tensor, y: torch.Tensor) -> torch.Tensor:
     output = torch.empty_like(x)

     assert x.is_cuda and y.is_cuda and output.is_cuda and x.shape == y.shape
     M, N = x.shape
     BLOCK_SIZE =  1024

     grid = lambda meta: (M, )

     add_kernel[grid](x,
                      y,
                      output,
                      M, N,
                      x.stride(0), x.stride(1),
                      BLOCK_SIZE=BLOCK_SIZE)

     return output

It is similar to the implementation in Part 1 except for the BLOCK_SIZE. Its now BLOCK_SIZE = 1024 instead of BLOCK_SIZE = triton.next_power_of_2(N).

Triton Kernel

For this implementation since the BLOCK_SIZE < N we will have to run a loop to keep loading BLOCK_SIZE worth of data and compute the addition until all elements in the row are read. Here’s the code:

@triton.jit
 def add_kernel(x_ptr,
                y_ptr,
                output_ptr,
                M, N,
                stride_m, stride_n,
                BLOCK_SIZE: tl.constexpr,
                ):
     row_id = tl.program_id(0)
     offset = tl.arange(0, BLOCK_SIZE)

     x_ptrs = x_ptr + row_id * stride_m + offset * stride_n
     y_ptrs = y_ptr + row_id * stride_m + offset * stride_n
     output_ptrs = output_ptr + pid * stride_m + offset * stride_n

     for i in range(0, tl.cdiv(N, BLOCK_SIZE)):
         x = tl.load(x_ptrs, mask=offset < (N - i * BLOCK_SIZE))
         y = tl.load(y_ptrs, mask=offset < (N - i * BLOCK_SIZE))

         out = x + y
         tl.store(output_ptrs, out, mask=offset < (N - i * BLOCK_SIZE))

         x_ptrs += BLOCK_SIZE
         y_ptrs += BLOCK_SIZE
         output_ptrs += BLOCK_SIZE

1. row_id = tl.program_id(axis=0) - Represents the row the kernel instance is operating on.
2. offset_n = tl.arange(0, BLOCK_SIZE) - Creating an offset list of the pointers within the block.
3. the for loop loads a block worth of data and computes the sum and stores at the output pointer locations. Below figure shows the sequence of operations for 0th row_id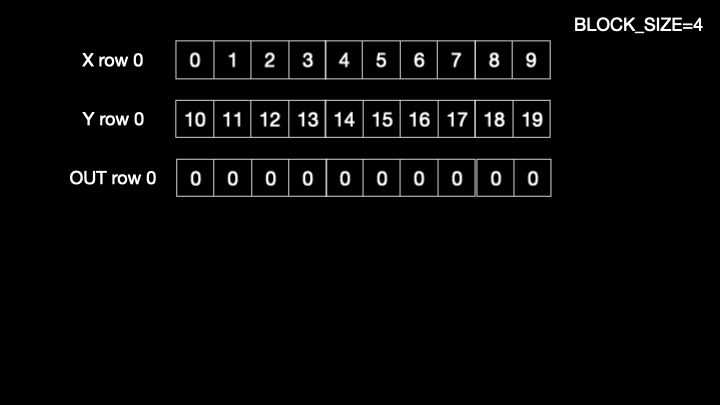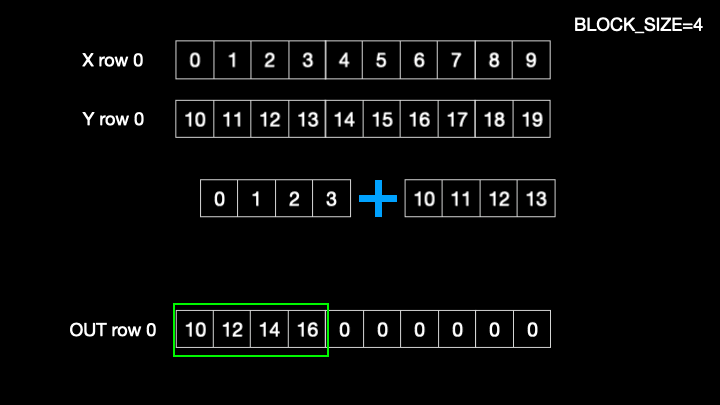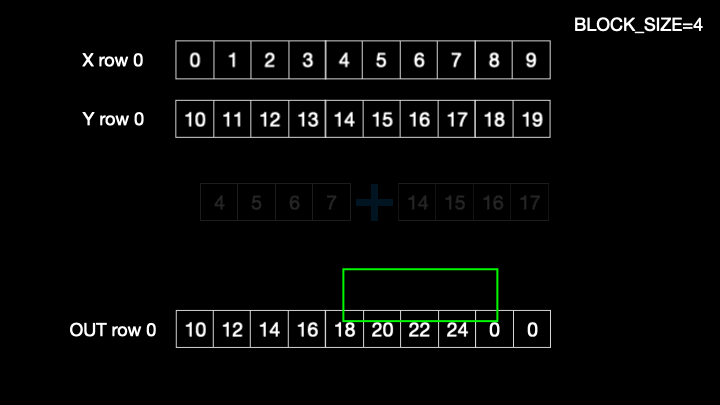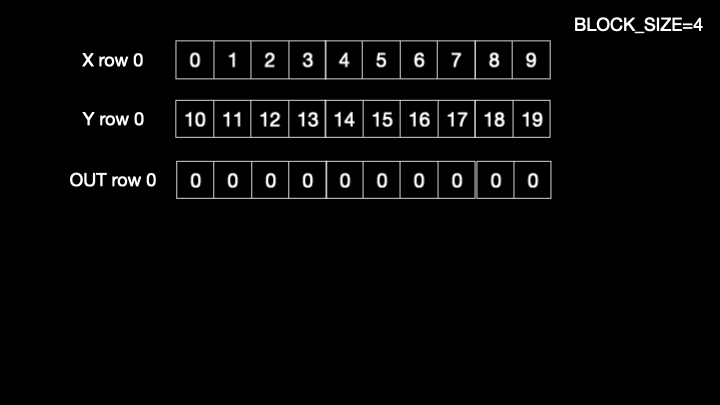 Fig1

Implementation 2 - Parallelize across Blocks.

Driver Function

In this implementation we will be parallelizing across BLOCKS. So the number of grids will be M * ceil(N, BLOCK_SIZE).

def add(x: torch.Tensor, y: torch.Tensor) -> torch.Tensor:
     output = torch.empty_like(x)

     assert x.is_cuda and y.is_cuda and output.is_cuda and x.shape == y.shape
     M, N = x.shape
     BLOCK_SIZE = 1024

     grid = lambda meta: (M * triton.cdiv(N, meta['BLOCK_SIZE']), ) # <-- # of Grids

     add_kernel[grid](x,
                      y,
                      output,
                      M, N,
                      x.stride(0), x.stride(1),
                      BLOCK_SIZE=BLOCK_SIZE)

     return output

Triton Kernel

Here’s the implementation.

@triton.jit
def add_kernel(x_ptr,
            y_ptr,
            output_ptr,
            M, N,
            stride_m, stride_n,
            BLOCK_SIZE: tl.constexpr,
            ):
    pid = tl.program_id(0)

    n_grids = tl.cdiv(N, BLOCK_SIZE)
    row_id = pid // n_grids
    col_id = pid % n_grids
    offset_m = row_id * stride_m
    offset_n = col_id * BLOCK_SIZE + tl.arange(0, BLOCK_SIZE)

    x_ptrs = x_ptr + offset_m + offset_n
    y_ptrs = y_ptr + offset_m + offset_n
    output_ptrs = output_ptr + offset_m + offset_n

    mask = offset_n < N
    x = tl.load(x_ptrs, mask=mask)
    y = tl.load(y_ptrs, mask=mask)
    out = x + y
    tl.store(output_ptrs, out, mask=mask)

Triton loads the BLOCK_SIZE worth of data from memory and then zeros out the part that’s outside the mask. The problem with this approach is its not bandwidth efficient for ROW_SIZE that are not power to 2. For smaller row sizes the effect is not much but for larger ROW_SIZE, the effect is significant.

Let’s take an example:

ROW_SIZE = 16385
BLOCK_SIZE = triton.next_power_of_2(ROW_SIZE) # -- > 32768

In this case BLOCK_SIZE - ROW_SIZE = 16383 are wasted elements which were loaded.