Vector Addition using OpenAI Triton - Part 1

This is the first blog in the series of blogs for implementing OpenAI Triton Kernels.

In this blog we are going learn how to write triton kernel for vector addition for a 2D matrix.

Basics

Triton is a blocked programming language. This means every operation in the program is happening on a block of data. For simplicity, we can think that only a single thread is doing all the work within the block. However the block itself is going to be parallelized by the compiler. User still has some flexibility to control the parallelism by specifying the number of warps (will be covered in future blogs). For the most part parallelism inside the block is hidden which is what makes it different from CUDA.

Triton language deals with pointers. The following are going to be common to pretty much all triton kernels

1. Pointer to the input tensor
2. Pointer to the output tensor
3. BLOCK_SIZE

It is going to be the users responsibility to create the pointers for the elements in the block which will be loaded from memory and operated on. Let’s understand offset calculation before delving into the actual kernel code.

Offset Calculation

As mentioned before, Triton is a block programming language. Let’s familiarize with Grids and Blocks. Say A is tensor of size N . Let the BLOCK_SIZE be K where K < N. Then, num_grids is the number of instances of the kernel that will be running in parallel. It is computed as

num_grids = math.ceil(N/K)

Each of these instances are can be uniquely identified by an ID.

grid_id = tl.program_id(axis=0)

The starting offset for any block will be given by the following block_start_ptr = grid_id * BLOCK_SIZE.

Let’s look at the example below

Memory Layout

Here we have an array whose elements values are from 0 to N. BLOCK_SIZE is 4. If we want to compute the starting address of Grid4 then we have to 4 * BLOCK_SIZE

Now that we have the starting address of the block, next thing is to compute the addresses of every element in the block. This is done by following:

block_ptrs = block_start_ptr + tl.arange(0, BLOCK_SIZE)

tl.arange is equivalent of np.arange.

The result for the example above for grid4 will be:

block_ptrs = 4 * BLOCK_SIZE + tl.arange(0, BLOCK_SIZE) # 4 * 4 + [0, 1, 2, 4] => [16, 17, 18, 19]

This is how the offset is computed for a 1D array.

Driver Function

This is the function which serves the interface between the rest of the application and the triton kernel. Here’s an example of the driver function.

def add(x: torch.Tensor, y: torch.Tensor) -> torch.Tensor:
     output = torch.empty_like(x)

     assert x.is_cuda and y.is_cuda and output.is_cuda and x.shape == y.shape
     M, N = x.shape 
     BLOCK_SIZE = triton.next_power_of_2(N)
     grid = (M, )

     add_kernel[grid](x, # pointer to starting address of x
                      y, # pointer to starting address of y
                      output, # pointer to starting address of output
                      M, N, # Shapes
                      x.stride(0), x.stride(1), # Strides
                      BLOCK_SIZE=BLOCK_SIZE) 

Let’s breakdown the above code:

• assert x.is_cuda and y.is_cuda and output.is_cuda and x.shape == y.shape makes sure the tensors are already on the GPU.
• M, N = x.shape - Gets the shape of the Input tensor.
• BLOCK_SIZE = triton.next_power_of_2(N) - This is really important part. For this implementation we are going to be loading the entire row of the MxN matrix and computing the vector sum. To be able to load the entire row at once we have to set the size of the BLOCK_SIZE to be the size of the row. However, in triton we have a restriction of BLOCK_SIZE as power of 2. So we are going to set the BLOCK_SIZE to be the next power of 2 of the size of the row. Triton provides a convenient function for this - triton.next_power_of_2
• grid = (M, ) - Grid Shape. Tells triton how many instances of the kernel needs to be launched. Here its M because we are going to be parallelizing over rows.
• add_kernel[grid](...) - Call to triton kernel.
  • x, y, output - These are tensors but the compiler will pass the pointer to the kernel.
  • M, N- Shapes of the tensor.
  • x.stride(0), x.stride(1) - Stride for each dimension.
  • BLOCK_SIZE - User defined BLOCK_SIZE

Triton Kernel

 @triton.jit
 def add_kernel(x_ptr,
                y_ptr,
                output_ptr,
                M, N,
                stride_m, stride_n,
                BLOCK_SIZE: tl.constexpr,
                ):
     # 1. Get the kernel instance identifier.
     grid_id = tl.program_id(axis=0)
     
     # 2. compute the range for the block
     offset_n = tl.arange(0, BLOCK_SIZE)
     
     # 3. compute the pointers
     x_ptrs = x_ptr + grid_id * stride_m  + offset_n * stride_n
     y_ptrs = y_ptr + grid_id * stride_m  + offset_n * stride_n
     
     # 4. Load data from memory.
     x= tl.load(x_ptrs, mask=offset_n < N, other=0.0)
     y= tl.load(y_ptrs, mask=offset_n < N, other=0.0)
     
     # 5. compute vector addition.
     out = x + y
     
     # 6. compute output pointers
     out_ptrs = output_ptr + grid_id * stride_m + offset_n * stride_n

	   # 7. Store the computed output into memory at output pointer locations.
     tl.store(out_ptrs, out, mask=offset_n < N)

1. grid_id = tl.program_id(axis=0) - Gives the instance id of the kernel. In this case it identifies the which row the kernel is operating on.
2. offset_n = tl.arange(0, BLOCK_SIZE) - Creating an offset list of the pointers within the block.
3. x_ptrs = x_ptr + grid_id * stride_m + offset_n * stride_n
   • grid_id * stride_m - points to the correct starting address of each row. We have used stride_m instead of BLOCK_SIZE because BLOCK_SIZE doesn’t correspond to the row size.
   • offset_n * stride_n - creates the list of offset pointers in the block. (more on strides)
   • grid_id * stride_m + offset_n * stride_n - computes the list of offset pointers with correct row offset.
   • Adding x_ptr to the above equation gives the list of actual pointers to be accessed in the block.
4. x= tl.load(x_ptrs, mask=offset_n < N, other=0.0) - Loads the data from memory using the computed pointers. The pointers have been computed for the BLOCK_SIZE which is greater than the size of the row. So we have to create a mask to zero out the elements which are outside the range of the row_size.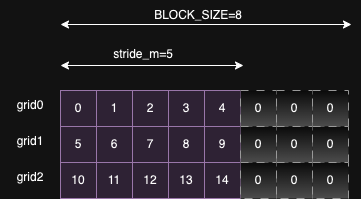
5. out = x + y - Vector Addition for the block.
6. out_ptrs - output pointers computation follows the same logic as input pointer computations in step 3.
7. tl.store(out_ptrs, out, mask=offset_n < N) - Writes the computed result back to memory for values that satisfy the mask condition.

Here’s the code to call the driver function and compare it to torch.

if __name__ == "__main__":
     torch.manual_seed(0)
     M, N = 101, 100001
     x = torch.rand((M, N), device='cuda')
     y = torch.rand((M, N), device='cuda')

     output_torch = x + y
     output_triton = add(x, y)
     logging.info(f'The maximum difference between torch and triton is '
           f'{torch.max(torch.abs(output_torch - output_triton))}')

Full code is available here

Summary

In this blog, I presented the following:

• Basics of Triton language.
• Offset calculation intuition.
• 2D Vector Addition kernel implementation

Next Post

• Implement 2D Vector Addition using
  • Implement with different BLOCK_SIZE. (BLOCK_SIZE < ROW_SIZE, 2D BLOCK_SIZE)
  • Implication of different BLOCK_SIZE on performance.

Resources

1. Triton Tutorial